SOLUCIÓN A: "LA PARADOJA DE LOS TRIÁNGULOS"

Triángulo superior

El triángulo superior no es un triángulo, es un falso triángulo.
La hipotenusa del triángulo ADF tiene una inclinación de 3/8=0,375.
La hipotenusa del triángulo DCE tiene una inclinación de 2/5=0,4.










Luego la hipotenusa del triángulo verde oscuro tiene más pendiente que la del triángulo rojo.
Por lo tanto la línea AC no es una línea recta, sino dos segmentos unidos.
(clic en las imagenes para ampliar)




Si trazáramos una línea recta desde A hasta C, no debería de pasar por el punto D, sino un poco más arriba, por fuera del falso triángulo superior.


Podemos trazar un triángulo (este sí es verdadero) ADC.

Triángulo inferior

El triángulo inferior tampoco es un triángulo, es un falso triángulo, tan falso como el superior.











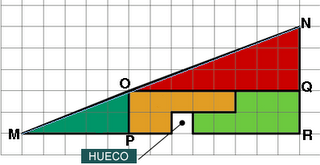
El triángulo MOP es el mismo que el DCE y el triángulo ONQ es el mismo que el ADF, por lo tanto las inclinaciones también serán diferentes.







Si trazáramos una línea recta desde M hasta N, no debería de pasar por el punto O, sino un poco más abajo, por fuera del falso triángulo inferior.
Podemos trazar un triángulo (verdadero) MON.



La suma de las áreas de los triángulos ADC y MON debe de ocupar exactemente una unidad, la unidad que ocupa el hueco que falta en el falso triángulo inferior.

Vamos a comprobarlo.

Trazamos un auténtico triángulo ACB. Si restamos al área de ACB el área de todas las figuras del falso triángulo superior obtendré el triángulo ADC.
Calculemos el área de ACB. S = (AB * CB)/2= (13*5)/2= 32,5.
Calculemos el área del rectángulo DEFB. S = DF * FB= 5*3= 15.
Calculemos el área del triángulo ADF. S =12.
Calculemos el área del triángulo DCE. S =5.

El área del falso triángulo es S = 12 + 5 + 15 = 32.
Si restamos esta superficie de la del verdadero triángulo tenemos la superficie del triángulo ADC: S = 32,5 - 32 = 0,5.

De forma análoga podemos calcular la supericie del triángulo MON. También es 0,5.

La suma de las superficies de los triángulos ADC y MON sería: S = 0,5 + 0,5 = 1.

Es decir la unidad que ocupaba el hueco que falta en la parte inferior.

El truco de este juego consiste en trazar las lineas que delimitan las figuras con bastante grosor para disimular el ya de por sí pequeño error que presentan los falsos triángulos.

Pero un pequeño error causa a veces efectos sorprendentes.