EL HOMBRE DEFORME

Creo que con este gif, queda clara la solución.

UN ACERTIJO NUMÉRICO

Lo que compra son números para ponerlos en la puerta de su casa. Uno (=1) cuesta 2 euros. Diez (=10), al llevar dos cifras, cuesta el doble: 4 euros. Doscientos (=200), al llevar 3 cifras, cuesta el triple: 6 euros.

SOLUCIÓN A: "UN ACERTIJO GEOMÉTRICO"

Si unimos el centro de la Tierra con la cima del monte El Jardón y con Uad Lau obtenemos un triángulo rectángulo. Esto es así porque si trazamos un circunferencia que pase por la base del monte El Jardón y por Uad Lau, el punto más lejano visible en el horizonte desde la cima del Jardón será Uad Lau. Por lo tanto si trazamos una línea que una la cima con Uad Lau, esta línea será tangente a la superficie terrestre, y formará un ángulo recto con la línea que pasa por el centro de la tierra y Uad Lau. Si la línea no fuera tangente o bien no podríamos ver Uad Lau o bien veríamos más al sur.

Tenemos el triángulo ABC. Si R = radio de la Tierra, H = altura del monte El Jardón y D = distancia entre el monte Jardón y Uad Lau.
CB = R
AC = R + H
AB = D

Por el teorema de pitágoras (R + H)² = R² + D²

R² + H² + 2RH = R² + D²

2RH = D² - H²

R = (D² - H²)/2H = (124,03² - 1,206²)/2*1,206 = (15383,4409 - 1,454436)/2,412
R = 15381,986464/2,412 = 6377,2746534

Me ha sorprendio que el resultado es casi casi el valor real de R.

SOLUCIÓN A: "LA PARADOJA DE LOS TRIÁNGULOS"

Triángulo superior

El triángulo superior no es un triángulo, es un falso triángulo.
La hipotenusa del triángulo ADF tiene una inclinación de 3/8=0,375.
La hipotenusa del triángulo DCE tiene una inclinación de 2/5=0,4.










Luego la hipotenusa del triángulo verde oscuro tiene más pendiente que la del triángulo rojo.
Por lo tanto la línea AC no es una línea recta, sino dos segmentos unidos.
(clic en las imagenes para ampliar)




Si trazáramos una línea recta desde A hasta C, no debería de pasar por el punto D, sino un poco más arriba, por fuera del falso triángulo superior.


Podemos trazar un triángulo (este sí es verdadero) ADC.

Triángulo inferior

El triángulo inferior tampoco es un triángulo, es un falso triángulo, tan falso como el superior.











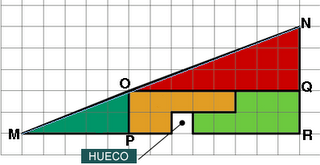
El triángulo MOP es el mismo que el DCE y el triángulo ONQ es el mismo que el ADF, por lo tanto las inclinaciones también serán diferentes.







Si trazáramos una línea recta desde M hasta N, no debería de pasar por el punto O, sino un poco más abajo, por fuera del falso triángulo inferior.
Podemos trazar un triángulo (verdadero) MON.



La suma de las áreas de los triángulos ADC y MON debe de ocupar exactemente una unidad, la unidad que ocupa el hueco que falta en el falso triángulo inferior.

Vamos a comprobarlo.

Trazamos un auténtico triángulo ACB. Si restamos al área de ACB el área de todas las figuras del falso triángulo superior obtendré el triángulo ADC.
Calculemos el área de ACB. S = (AB * CB)/2= (13*5)/2= 32,5.
Calculemos el área del rectángulo DEFB. S = DF * FB= 5*3= 15.
Calculemos el área del triángulo ADF. S =12.
Calculemos el área del triángulo DCE. S =5.

El área del falso triángulo es S = 12 + 5 + 15 = 32.
Si restamos esta superficie de la del verdadero triángulo tenemos la superficie del triángulo ADC: S = 32,5 - 32 = 0,5.

De forma análoga podemos calcular la supericie del triángulo MON. También es 0,5.

La suma de las superficies de los triángulos ADC y MON sería: S = 0,5 + 0,5 = 1.

Es decir la unidad que ocupaba el hueco que falta en la parte inferior.

El truco de este juego consiste en trazar las lineas que delimitan las figuras con bastante grosor para disimular el ya de por sí pequeño error que presentan los falsos triángulos.

Pero un pequeño error causa a veces efectos sorprendentes.

SOLUCIÓN A: "OTRO ACERTIJO ZOOLÓGICO"

¿Dificil? La polilla se encuentra justo en el centro de la imagen, marcada con la letra F. Aquí la tenemos un poco más cerca.



¿Aún no la ves? Mirémosla ahora desde atrás. Si te fijas bien se observan las patitas de la polilla.

SOLUCIÓN A: "UN ACERTIJO ZOOLÓGICO"

Esta especie es Parasemia plantaginius, la mariposa del número 4.


Esta es Colias philodice, la mariposa del número 8.

Si Parasemia plantaginius = 4 y Colias philodice = 8, entonces:

A = Parasemia plantaginius * Colias philodice + Colias philodice = 4 * 8 + 8 = 40

y B = A + A + Colias philodice = 40 + 40 + 8 = 88

La mariposa del número 88 es Diaethria clymena